[에라둔] 역학 문항에서의 미래와 과거
계산적으로 중요한 내용들은 아니고 그냥 편히 읽으시면 될법한 내용들입니다.
역학 문항을 풀다 보면 여러가지 상황을 마주하게 되는데
종종 동일한 카테고리를 마주하게 됩니다.
이번에 다룰 내용은 어찌보면은 상대속도와 조금 관련이 있을 수 있습니다만 일단 접어두고.
아래 문항들의 공통점이 무엇일까요?

20230618


20210911


20130920
세 문항의 공통점은 두 물체가 모든 지점에 대하여 운동 방향, 속력 모든것이 동일한 상황들입니다.
이전에 저도 문항 출제를 할 때 위와 같은 상황을 이용하여 문항 출제롤 하곤 했는데
위와 같은 문항을 출제하면 참 좋은게 v-t그래프를 옆으로만 삭 밀어주면 되기 때문에
검토하기가 수월해서 즐겨냈었던 기억이 어렴풋이 납니다.
거두절미하고
어떻게 보면 위와 같은 문항들은 상대속도를 활용할만한 문항들 중에서도 특수한 케이스라고 생각을 하는데
저같은 경우에는 두 물체에 대하여 가상의 시간차 t를 가정하고 문제 풀이를 하는것을 선호합니다.
뿐만 아니라, 시간차 t가 난다고 생각하고 문항을 바라보면 좀더 문제 상황을 직관적으로 파악하기도 좋지요.


예를 들어 위 문항의 경우엔 B의 2초 뒤 모습이 A라고 생각하면서 풀면 문제 풀이가 아마 수월하겠죠.
일단 ㄱ이 바로 나올것이며
2초뒤 B가 정지할테니 평균속력 2라는 점에서 v=4가 바로 나올것이며
dv=4인동안의 시간이 2초니 가속도가 2인것도 술술 나올것입니다.


20210911
마찬가지로 위 문항도 B가 t초뒤의 A모습이라고 가정한다면 3vt=L이 나올것이며
우리는 자연스레 A가 p에서 q까지 이동하는데 걸리는 시간이 t라고 할것이기에
평균 속력 공식을 이용하여 1.5vt=0.5L과 같이 문항들이 순둥순둥하게 풀릴것입니다.
위와같이 동일한 경로, 운동 상황을 공유하는 문항의 경우에는 결국엔 대부분 문항에서 요구하는것은
두 상황에 대한 연립일것이며, 이 연립과정이 가감의 과정이기 떄문에
사실 t로 두고 문항을 풀면 쉽게 풀리는 경우가 많습니다.


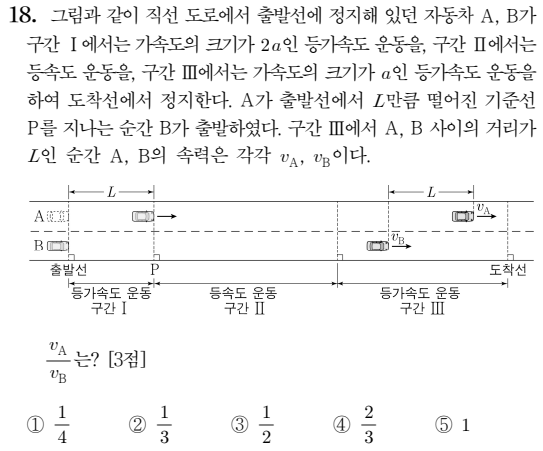
20230618
위 문항의 경우에도 마찬가지로 역시 B의 t후 모습이 A라 생각하고 풀면 풀기가 수월할것입니다.
등가속도 운동 구간 I에서의 가속도를 2a라 하면 (0+2at)t/2=att=L이 나올것이며
이후 vb인 B가 시간 t 후 속력이 va가 된다고 하면 자연스레 (va+vb)/2 * t = L이 나오게 될것입니다.
그리고 구간 3에서 시간 t동안 속력이 변하였는데 이것이 va-vb일지 vb-va일지는 잘 모르겠습니다.
사실 시간 t라는 차이를 생각해보면 B가 출발할 때 이미 가속된 A가 있기에 거리차가 L보다 벌어질텐데
다시 L로 감소했다는 포인트를 보면 아마 가속도가 감소했음을 알기 수월하겠지요.
그러한 이유로 (va+vb)=2L/t, (vb-va)=at=L/t
va+vb : vb-va = 2:1, 2vb-2va = va+vb, 3va=vb, va:vb=1:3 이 나오게 될것입니다.
저같은 경우에는 두 물체가 동일한 경로를 운동하면 습관적으로 동일한 운동까지 하는지를 체크합니다.
아마 위와같은 유형들을 깔끔하게 푸시는 분들이라면 위의 개념을 숙지한 상태에서
그 이상은 본인의 직관, 암산 등으로 인한 최적화 정도의 차이만이 존재할것입니다.
만약, 위와 같은 수식적 풀이가 다소 어렵다면 그냥 모든 시간 영역을 t미지수로 두고 풀어보시거나
vt 그래프를 정성스럽게 그려보시는것을 권장드립니다.
아마 그래프를 그리시다 보면 자연스레 평행사변형과 친해지게 될겁니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
탈급간 아님? 취업률도 그렇고 ㅇㅇ
-
오늘의 모닝 실모 결과 11
한수 파이널 7차: 87 이해원 파이널 1회:96 국어... 90점대가 실종됐다
-
오늘 밤샐거임 7
ㄹㅇ임
-
국숭세단: 일반인도 이름은 다 들어봄 광명상가: 수험생한테는 익숙함 한서삼: 무슨...
-
40분안에 풀기 가능인가요???
-
그뒤로 나락갔는데 수능때 커하 ㄱㄴ?
-
그냥 여친분 부러워ㅓㅓㅓㅓㅓㅓㅓㅓㅓㅓ
-
거의 다 여자임 남자는 카리나 윈터가 있는데 굳이 닝닝이 이쁘다 하지 않음
-
냥냥 10
찐친랑 저나하는데 별 이상한 인간들이 너무 많네 사람 진짜 오래봐야대 요즘 더 그런거가타
-
디자인에서는 연고대급인데 일반계열은 그게 아닌게 현실이라 국민대 가고싶다하면...
-
겨울 때 못들은 단과영상, 파이널단과 영상 찍어둔거 안들었는데 이거 아깝다고 들을...
-
대 방 어 4
대 대 대
-
22 30맞 20 9 틀....
-
ㄴ선지 ㄷ선지가 궁금한데요 ㄴ선지는 그림 A-B가 용융점(?)을 넘기기 못해서...
-
근데 서/연고도 2
연대 경영 성적으로 서울대 협문 못들어가지 않음? 고경은 몰루
-
60후반에서 80초 진동하는데 많이 풀기 전에 본 6모가 80점이었거든요.....
-
??
-
실력이 뒷받침되어야하는건 맞지만 요새 개인적인 일로 우울감이 많아졌는데 이게 하필...
-
여산의 진면목이 여긔야 다 뵈는다 라는 문장을 보고 어떻게 여산이 중국의 산인걸 알수 있을까
-
갤러리 구경하다 발견함
-
연경제 고경제 둘 다 붙으면 어디 가실거임?
-
모고 문제도 해설도 답지도 뭔가 엉성해
-
전 라인 통틀어서 이 벽만큼 큰 라인은 솔직히 없음 상대적으로 다른 라인에 벽이...
-
ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ
-
어떨때는 적게 자도괜찮아 어느때는 자도자도 피곤함
-
건동홍부터는 붙여주면 절 몇번 넙죽 해드리고 기어서 들어갑니다~
-
탈출하겠다는일념.
-
좋은가요 8시간정도?
-
국어 4 수학 5 탐구 11로 동홍이 된다고 누가 그러는데 ㅇㄱㅈㅉㅇㅇ????
-
11투스 0
다들 미적 난이도 어떤가요? 그냥 적당한거임?
-
응디쿄쿄이 0
광활한 천구 안의 작은 점 하나
-
251122 미리보기 10
22번 수1 내줬잖아 6,9평도 22번 수열냈으니까 통수아니지? 그치? 근데,...
-
명문은 연고까지 3
반박시 내말이 다 맞음
-
문과누백 << 이건 문과들끼리 줄세운거고 이과누백 << 이게 이과들끼리...
-
건동홍도 명문임 12
반박은 안받음
-
어렵다는 모의고사인데 사실 작년 수능이 더 어려웠음 수능 전에 본 모든...
-
평소에 화장 하는데 아예 안하고 보정 없이 아이폰 16 기카로 찍은 사진인데 님들이...
-
한숨잘까 1
-
이대봉전 6
6평 이대봉전 정도면 난이도 좀 있는 고전소설 아닌가요..? 왤케 정답률이 높지
-
네 저예요
-
이감 수능 0
이감은 60~70점대 오늘 친 23수능은 90점대 뭐가맞는지 모르겠다
-
반수 성공한다는데 지금 대학도 높아보임 ㅋㅋ
-
6평 9평 미응시 삼반수생 어둠의 표본인 ‘나‘가 참전하기 때문.
-
수능수학 10
언제쯤 귀납적 수열이 안나올까 ㄱㄴㄷ, 무등비 삼도극 이런애들은 없애면서 왜 귀납...
-
내가 그렇게 만들거임 사실 그런건 아니지만 굳이 명문대 급 나누고 상처받는 것보단...
-
0도 아니고 내맘대로 3/2라고 생각함
-
【파이낸셜뉴스 전주=강인 기자】 전북지역 거점 국립대인 전북대학교가 단순한 학교...
-
싫은데? 안풀건데?
-
ㅅㅂ 10덮 풀어봤는데 더 쉬운것들보다도 더 좆망한 점수가 나옴



















































옆동네 옆옆동네에서 잘 보고 있습니다감사합니다!!
와 쌤 과외 받았던 학생인데,,, 잘 계시나요 ㅠㅠ
감사했습니다!! 덕분에 카이스트 가서 잘 지내고있어요