2020년 10월 모의고사 수학 가형 30번 해설
오늘은 한달 전 시행됐던 10월 모의고사 수학 가형 (이과) 30번 문제 풀이방법에 대하여 알려드리겠습니다.
단순히 한 문제에 대한 풀이로 마치는 것이 아니라 문제를 푸는 근본적인 방법에 대하여 조언해드리니, 킬러문제가 고민이신 분들은 꼭 칼럼을 꼼꼼히 읽어주세요.
먼저 2020년 10월 모의고사 수학 가형 30번 문제를 소개합니다. 아직 문제를 풀어보지 않은 분들은 반드시 풀이를 보기전에 스스로 문제를 풀어보세요.
다음으로, ebsi에 수록되어 있는 공식 풀이방법을 소개해드리겠습니다.
물론 쉬운 문제는 아니였습니다. 그러나 킬러문제중 가장 어렵기로 유명한 30번의 평균 난이도를 고려하면 다른 30번들 보다는 쉬운 편이라 할 수 있습니다.
따라서 30번에 도전하려는 마음가짐으로 이 칼럼에 들어오신 여러분들이라면, 스스로 풀지는 못했더라도 답지 풀이 정도는 충분히 이해하실 수 있을 것입니다.
그러나 항상 가장 중요한 것은 단순 이해를 넘어서, 비슷한 문제가 나오면 내가 스스로 풀 수 있을지, 풀이를 온전히 내 것으로 만들 수 있을지 생각해 보는 것입니다.
지금부터 풀이과정을 하나씩 구체적으로 살펴보며 풀이를 여러분의 것으로 만들 수 있도록 도와드리겠습니다.
첫번째로, f(0) = f(-2)임을 문제에서 제시했습니다. 이차함수이기 때문에 숙련된 분들은 성질을 이용하여 f(x) = kx(x+2) + q 라고 바로 잡을 수 있을 것입니다.
그러나 제가 바람직하다고 평가하는 합리적인 풀이는, 공식 답지처럼 조금 돌아가더라도 "누구나 생각해낼 수 있는 아이디어"입니다.
따라서 바로 식을 잡기가 어렵더라도, f(x)에 0,-2를 대입하여 식을 전개해도 전혀 문제가 없으며 동일한 결론을 유도해 낼 수 있습니다.
첫번째 과정을 통하여 p를 k에 대하여 나타내는 데 성공했습니다. AB < 0 의 형태가 나왔네요. 따라서 두번째로 -1을 기준으로 x 의 범위를 나누는 것은 당연합니다.
아마 대부분의 분들이 아직까지는 의문이 들지 않을 것입니다. 문제는 다음 파트에서 발생합니다.
풀이 자체를 이해하는 분들은 제법 계실 것입니다. 그러나, g'(-1)=-2을 구하는데 갑자기 g', g"을 구하는 이유는 무엇인가요?
그리고 비슷한 문제가 나왔을때 우리는 똑같이 논리를 전개하여 문제를 풀어낼 수 있을까요? 지금부터는 합리적인 논리 전개 방법에 대하여 말씀드리겠습니다.
첫번째로, 우리는 우리가 유도한 이 식을 어떻게 사용할지 고민해봐야 합니다. g(x)가 x = -1의 전후로 mx+m이라는 식과 부호가 바뀌려면 어떻게 해야할까요?
우선 x에 -1을 대입해 g(-1) = -m+m 값이 나와야 합니다. 그래야 부호가 바뀔 수 있는 최소한의 조건이 만족됩니다. 즉 첫번째 식 g(-1) = 0 이 유도됩니다.
그러나 여기서 우리는 하나의 식을 더 생각해내야 합니다. 왜냐하면 g(-1) = 0 은 필요조건일 뿐이지, g(-1) = 0 이라고 해서 주어진 부등호가 반드시 성립하는 것이 아니기 때문입니다.
여기에 식을 만족시키려는 m의 최소값이 2라는 힌트가 주어져 있습니다. 즉 이 식을 이용하여 추가 조건을 구하라는 것을 깨달을 수 있습니다.
저는 이후의 풀이는 공식 풀이와는 조금 다른 방식으로 해결했습니다. 생각해보세요. -1을 기점으로 mx+m와의 대소가 변하려면 어떻게 해야할까요?
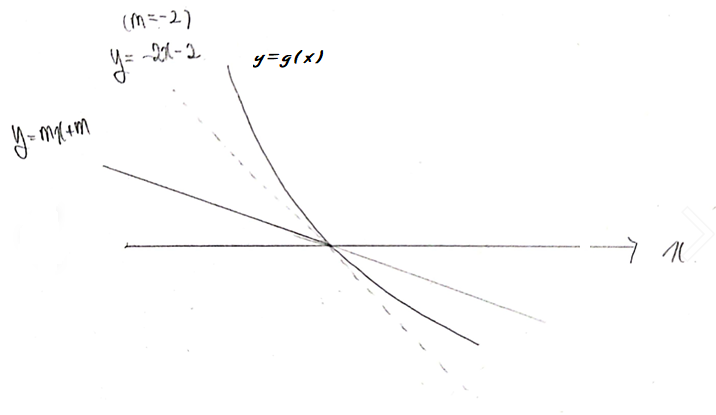
반드시 그림과 같은 형태가 나와야합니다. 즉 함수값이 같은 것 뿐만 아니라 반드시 m이 g'(-1)보다는 크거나 같아야 한다는 것이죠. 이때 m의 최소값이 -2이므로, g'(-1) = -2 가 되는 것은 자명합니다.
이제 두 식을 연립하여 다음 식을 유도할 수 있습니다.

이 식은 문자 3개, 식1개의 형태입니다. 즉 2개의 식만 더 있으면 문제를 풀어낼 수 있습니다. 이제 (나)식을 한번 살펴볼까요?
(나) 조건은 딱 두개의 식을 구할 수 있도록 되어 있습니다. 또한 g(x)는 지수 위의 식을 미분하면 아래의 함수가 나오는 형태기 때문에, 매우 적분하기 쉽습니다.
따라서 이제 문자 3개, 식3개, a,k,q를 모두 구할 수 있다는 것입니다. 문제의 풀이를 단순히 쭉 읽어봤을때는 스스로 풀기가 어렵다고 생각할 수 있습니다.
그러나 하나씩 과정을 살펴보며 왜 이런 아이디어를 사용 할까?에 초점을 맞추어 복습을 한다면, 문제를 푸는 것이 점점 쉬워진다는 것을 느낄 수 있습니다.
여러분들 스스로도 "내가 왜 이러한 방식으로 논리를 전개해나가고 있을까" 라는 질문을 스스로 던지며 문제를 풀어보세요. 근본적인 실력이 크게 향상될 것입니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
둘중에 하나민 넣을거 같은데 둘다 안정임
-
취업 면에서 어디가 그나마 낫나요? 상경에는 뜻이 없어서 둘 다 비상경이라고 할 때
-
그래서 정시한테는 언제풀어줄랑가 이렇게 좋은 학과를 양자컴이 미래다
-
이번에 한달전에본 2025수능도 서울대 연세대 고려대 세개만 내신반영이고 이제...
-
진짜 안할거냐 2
진짜 원서 전날에 퇴근했다고???
-
러시안 룰렛이랑 다르게 확률이 5/6임
-
아 힘들다 0
좀 쉬어야겠다
-
12시전에 되겠지…?
-
아주대식 905입니다 자전이랑 모빌 둘다 쓸건데 자전은 힘들어 보여서요ㅠㅜ
-
너무 그냥 슬퍼 2
잘가
-
오르비 2
내리비 오르락내리락
-
경희 글커 경희 체육 동국 열린전공 이렇게 쓰려고 하는데 7칸 6칸 6칸이라 만약에...
-
서울대 : 1-1 휴학 가능 카이스트 : 1-1 휴학 가능 연세대, 고려대 :...
-
매일 내 앞으로 10명씩은 들어오는 느낌..
-
???
-
사탐 vs 과탐 (공부 시기 관련, 무료배포 이벤트) 0
안녕하세요, 생명과학1을 가르치는 강사 권희승입니다. 오늘은 많은 분들이 고민하는...
-
현재 건동홍 낮공 다님
-
정모 열어주세요. 그리고 저랑 사겨주세요.
-
적지 흠
-
아케인 3
라이즈
-
의뱃 달았다 3
헤헤
-
돌격대장 우상혁 2
요즘 머하실까
-
훠훠 0
진학사 아직도 업뎃 안됐네
-
왜 떨리지 4
남자 보러가는건데
-
진학사 7칸추합 4
5명만 뽑는 소수과라 그런지 7칸으로도 추합이 뜨는데 이거 발뻗잠까지는 아니겠죠? 나군이에요
-
경희대 정디플 0
취업 잘되나요....?
-
지기균과 기균입니다 출처: 2025 기균 정보공유방
-
일개 회사가 입시판을 좌지우지 하는게 맞냐 없애라 ---> 업뎃 안함
-
다군은 안정박고 서울가야하니 가나군 중 하나에 건동 안정쓰고싶은데 스나가 될 과가...
-
차라리 표본 그득그득에 4칸이면 내가 포기라도 해볼게 4
18명 뽑는 과에 22등인데 냅다 4칸 주면 내가 납득이 안가지 않을까? 아 물론...
-
난 대성패스가 조아
-
제발 나오라예~ 0
나와라이저~
-
성인방송 광고글인가 그거 처리하는데 잠을 못 자서 실수하셨다 하시네요... 항상...
-
이걸 치워야하나 ㅅㅂ.. 치워도치워도 더러운데 내일 부모님 오심..
-
나 여잔데 결혼하기는 싫음 근데 귀여운 여자아이 입양해서 예쁘게 잘 키우고싶다.....
-
올해 커리 정함 5
다 과외할거임 국어 : 아케인 라이즈 수학 : 하니의벽 영어 : 연화숫으 쌍사 : 셀프 과외 ㅁㅌㅊ
-
해명해
-
알바가기 싫다 0
엄마랑 놀때가 재밋엇는데
-
대성패스 내일까지네 다시.. 해볼까?
-
1년반 넘게 반성했는데 한번만 봐주세요........흑흑
-
성적 경고가 뭐지..
-
이러다간 다 죽을텐데
-
ㅠㅠ
-
제가 패스를 좀 늦게 구매해서 잡도해를 지금 시작하게되었는데 잡도해를 들으면서 생글...
-
한의대 수시반수긴 한데 국영탐 최저 3합4이고 탐구는 사회문화 윤성훈t 들을...
-
아직도 안 하면 뭐하자는 거임
-
진학사 칸수 0
같은학교 비슷한 과 비슷한 인원 비슷한 추합인데 한 과는 4칸을 64명 주고 다른...
-
지금은 나혼자 연습하고 있긴 한데 누가 평가질을 좀 해야 감이 잡힐듯
-
믿어도 되나요...? 일반은 진학사 / 농어촌 김영일 기준이에요
-
나밖에 없음?






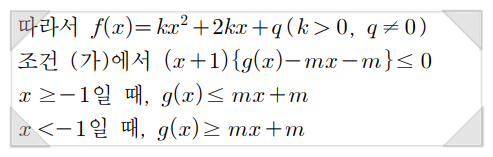

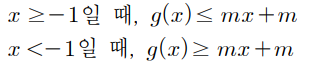

















































이따가 공부 끝내고 읽어볼게요